Qu'est-ce que l'algèbre de Boole et son rôle en informatique ?
L'algèbre de Boole a été inventée par le mathématicien anglais George Boole. Elle permet de réaliser des circuits effectuant des opérations très complexes à partir de composants simples tels que des transistors, qui sont les principaux éléments d'un processeur.
Le but principal est de traduire des signaux en expressions mathématiques. Pour cela, on définit chaque signal par une variable logique et son traitement par des fonctions logiques.
Les tables de vérité servent à définir les opérations que l'on veut effectuer et à écrire le résultat sous forme d'équation algébrique. Dans un circuit appelé « circuit logique », on schématise les effets des composants de base sans se préoccuper de leur réalisation matérielle.
Comment fonctionne la logique binaire sur un ordinateur ?
Tout le monde sait qu'un ordinateur ne se sert que de données binaires. On appelle cela des variables logiques qui ont seulement deux états possibles : 0 et 1.
Une fonction logique est une entité acceptant plusieurs valeurs logiques en entrée et dont la sortie n'a que deux possibilités : 0 ou 1.
Dans la réalité, ces fonctions logiques sont des composants électroniques recevant des signaux électriques en entrée et restituant un signal en sortie.
Exemple :
- Si on applique un courant de 15 V, le voyant s'allume (1).
- Si on applique un courant de 0 V, le voyant reste éteint (0).
Portes logiques ET, OU, NON : définition et fonctionnement
Les fonctions fondamentales sont appelées « portes logiques ». Elles peuvent avoir jusqu'à 2 entrées et disposent d'une seule sortie.
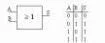
La porte OU (OR)

Elle positionne sa sortie à 1 si au moins une des entrées est égale à 1.
- Symbole : « ≥1 » (supérieur ou égal à 1)
La porte ET (AND)
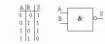
Elle positionne sa sortie à 1 si ses deux entrées sont à 1.
- Symbole : « & »
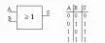
La porte OU EXCLUSIF (XOR)
Elle positionne sa sortie sur 1 si une seule de ses deux entrées est égale à 1.
- Symbole : « = 1 »
La porte NON (NOT)
Elle positionne sa sortie sur 1 si l'entrée est 0, et vice versa.
Il existe aussi les portes NON-OU (NOR) : il faut qu'aucune variable ne soit égale à 1 ; et NON-ET (NAND) : il faut que les deux entrées ne soient pas égales à 1.
Notation algébrique des fonctions logiques
Chaque fonction logique possède sa propre notation algébrique :
- OU : représentée par « + »
- ET : représentée par « . »
- NON : représentée par une barre au-dessus de la variable
- OU EXCLUSIF : représentée par un « + » entouré
J'espère que cet article vous aura plu et qu'il aidera ceux qui font ISI en seconde, les 1°S SI, ou tous ceux qui étudient les sciences de l'ingénieur !


